Options Pricing
Introduction
There are several models used for pricing options. Binomial tree and Black-Scholes are the most common models. The current stock price , the option strike price
, Maturity lenth
, risk-free interest rate
, volatility
are common factors for both models that determine the price of the option.
For instance, if the stock price rises, there is high probability that the price of a call option will rise and the price of a put option will fall. If the stock price goes down, the reverse will most likely happen to the price of the calls and puts. Intrinsic value is the amount by which the strike price of an option is in the money. It is the portion of an option’s price not lost due to the passage of time.
Binomial Tree model
Return to Top
In this model, consider a stock (with an initial price of undergoing a random walk. Over a time step
, the stock has a probability p of rising by a factor u, and a probability 1-p of falling in price by a factor d. This is illustrated by the following diagram.
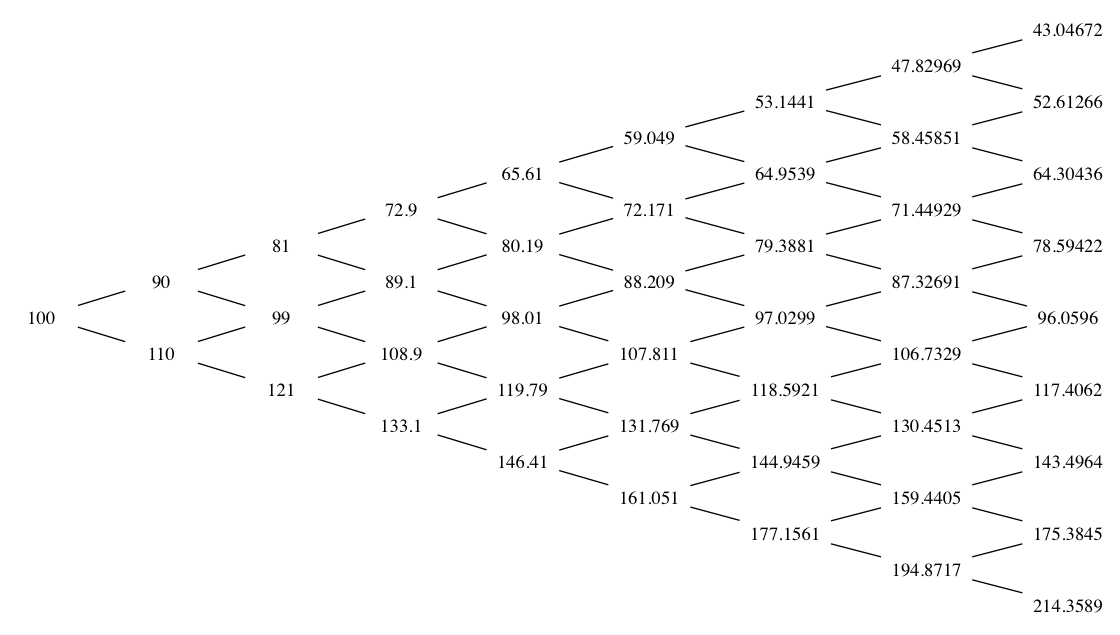
Cox, Ross and Rubenstein (CRR) suggested a method for calculating p, u and d. Over a small period of time, the binomial model acts similarly to an asset that exists in a risk neutral world. This results in the following equation, which implies that the effective return of the binomial model (on the right-hand side) is equal to the risk-free rate:
Additionally, the variance of a risk-neutral asset and an asset in a risk neutral world match. This gives the following equation.
The CRR model suggests the following relationship between the upside and downside factors.
Rearranging these equations gives the following equations for p, u and d.
The values of p, u and d given by the CRR model means that the underlying initial asset price is symmetric for a multi-step binomial model.
We will consider the following payoff functions at maturity time.
For call option:
For put option:
Also, the value of the option at each node can be computed using the following equation:
The above equation implies that we need to initially calculate the option price at maturity time (last node), and then move backwards to calculate the option price of each node until we reach today’s date (first node). The code for such algorithm in Python is given below:
import numpy as np
import scipy.stats as si
# N = number of nodes
# T = maturity time
# S = stock price
# K = strike price
# r = risk-free rate
# sigma - volatility
# options - call or put
def bionomial_tree(N,T,S,K,r,sigma, options) :
# delta T
dt = T/N
# caculate up,down and probaility
u = np.exp(sigma*np.sqrt(dt))
d = 1/u
p = (np.exp(r*dt) - d)/(u-d)
#create a matrix M for stock prices
M = np.zeros(shape=(N+1,N+1))
# set inital stock price
M[0,0] = S
# set-up parameters for calculating stock prices
a = 1
c = 2
up_N = 0
down_N = 0
# calculate stock price for each node
for x,i in enumerate(range(1,N+1)):
up_N = x + 1
down_N = 0
for j in range(0,c):
M[j][a] = S*u**(up_N)*d**(down_N)
up_N = up_N - 1
down_N = down_N + 1
a = a +1
c = c +1
# calculate the option price based on the stock price
if options == 'call' :
option = np.zeros([N+1,N+1])
option[:,N] = np.maximum(np.zeros(N+1),M[:,N]-K)
if options == 'put' :
option = np.zeros([N+1,N+1])
option[:,N] = np.maximum(K-M[:,N],np.zeros(N+1))
for i in np.arange(N-1,-1,-1):
for j in np.arange(0,i+1):
option[j,i] = np.exp(-r*dt)*(p*option[j,i+1]+(1-p)*option[j+1,i+1])
# return option value at time start time
return round(option[0,0],4)
Black-Scholes model
The Black-Scholes model is used to determine the price of a European call option, which simply means that the option can only be exercised on the expiration date. Black-Scholes pricing model is largely used by option traders who buy options that are priced under the formula calculated value, and sell options that are priced higher than the Black-Schole calculated value.
The formula for calculating the option price is:
The Python code for Black-Scholes is:
# T = maturity time
# S = stock price
# K = strike price
# r = risk-free rate
# sigma - volatility
# q: - divedn yeild
# options - call or put
def black_scholes(S, K, T, r,q, sigma, option):
d1 = (np.log(S / K) + (r - q + 0.5 * sigma ** 2) * T) / (sigma * np.sqrt(T))
d2 = (np.log(S / K) + (r - q - 0.5 * sigma ** 2) * T) / (sigma * np.sqrt(T))
if option == 'call':
result = (S * si.norm.cdf(d1, 0.0, 1.0) - K * np.exp(-r * T) * si.norm.cdf(d2, 0.0, 1.0))
if option == 'put':
result = (K * np.exp(-r * T) * si.norm.cdf(-d2, 0.0, 1.0) - S * si.norm.cdf(-d1, 0.0, 1.0))
return round(result,4)
Conclusion with example:
As an example, I will get the price of the call option for APPLE Inc. (AAPL) using both models. The current stock price , The option strike price
, and the volatility
for a 35 days maturity time (Expiration date Aug 16, 2019) obtained from YAHOO finance website on July 11, 2019 are 201.75, 200, and 26.22%, respectively. The Bid and Ask price shown on YAHOO is between 7.5 and 7.6 after market close. If we assume that the risk-free interest rate is 1% and there are no dividends, the option call price based on the Black-Scholes model is 7.72. Assuming that we choose 100 nodes for the Binomial Tree, the option call price is estimated at 7.73.
N = 100
T = 35
S = 201.75
K = 200
sigma = 0.27
r = 0.01
q = 0
option = 'call'
black_scholes(S, K, T, r, q, sigma, option)
binomial_tree(N, T, S, K, r, sigma, option)
It can be seen that the binomial pricing method and the black-scholes pricing method produce almost identical results when the dividend yeild for the black sholes pricing method is equal to zero. Given the nature of the code it is more efficient to use the black-scholes method of calculating the price of options becuase the binomial tress require 100 iterations which takes up more processing power and takes longer. With iterations less than 100 the bionomial tress method was seen to be less accurate. When dividends are factored into the black-scholes method it can be seen that the price of the options changes slightly.
To see the code in a Jupyter Notebook click the link below.